I am a backer of the upcoming Elite Dangerous game and have participated in their premium beta programme from the beginning, positively enjoying what was there at the early time. ‘Premium beta’ sounds like an oxymoron, paying a premium for an unfinished game, but it is nothing more than purchasing the same backer status as that from the Kickstarter campaign.
I came into contact with the original Elite during christmas in 1985. Compared with the progress I made back then in just two days, my recent performance in ED is lousy; I think my combat rating now would be ‘competent’.
But this will not be a gameplay review, instead I’m going to share thoughts that were inspired while playing ED, mostly about graphics and shading, things like dynamic range, surface materials, phase curves, ‘real’ photometry, and so on; so … after I loaded the game and jumped through hyperspace for the first time (actually the second time), I was greeted by this screen filling disk of hot plasma:
Solar Irradiance
Holy! The above screenshot shows a situation right after dropping out of hyperspace. I am supposed to be at a distance of 12.76 light seconds (3.8 million kilometers) to Theta Boötis, a class F star which is slightly hotter than our sun. I think people really underestimate the sheer intensity of solar radiation. Take a guess: at this distance, and in the absence of some fantastical heat blocking technology, how much time would a spaceship have to live before it begins to evaporate?
- hours
- minutes
- seconds
- you are crazy, it would not evaporate
The answer would be a few minutes. Just for fun I calculated the irradiance at this distance to be about 9 million watts per square meter! Under this power it would take 2 minutes to heat one tonne of iron to 2500 K (see [1] and [2] for the details of this calculation).
I’m not criticizing here. A game that allows to ’super cruise’ might as well postulate some technology for coping with close stellar proximity. But I think it should have to be outfitted explicitly and be very expensive, maybe even alien technology of Thargoid origin or something.
By the way, look again at the above screenshot. There is white glowing hot plasma, dim cockpit lights and even background stars in the same exposure? That’s a mighty dynamic range! Here comes the cue: Dynamic Range.

Dynamic Range
To elaborate about dynamic range, I choose a less extreme example, but still very educational. The second screenshot, taken from an early release, shows the fictional planet ‘Azeban’, which is supposed to be in the Gliese 556 system. Targeted in the background is the system 44 Boötis, at a distance of 5.47 light years.
To recapitulate: We have a sunlit planet and background stars in the same exposure. The ice sheet of the planet is just as bright as if you were actually standing on the planet looking at the glaring white snow around you. The stars are just as bright as ordinary night-sky stars. Take another guess: How many EV (exposure values) difference are between the snowy ice sheet (marked with A) and the faint star in the distance (marked with B)?
- 3
- 13
- 9600
- nitpicker, the image is fine as it is
I calculated the answer to be 13.2 EV, see [3] and [4] for the details of that calculation. EV is a logarithmic scale, so the corresponding linear factor would be about 1:9600 (haha I put a distractive answer into the multiple choice question). Put another way: if the region marked in A has an RGB color of #BFA575 then the star in B should be rendered as a single pixel somewhere in the range of #000000 to #030303, see [5] for that calculation.
The corollary is that really the background stars should be almost invisible in the same exposure together with other sunlit objects, like a planet. Only if the planet scrolls out of view, then you should be able to see stars (after some adaptation time). I also know that it is a common sci-fi trope to show stars when it is absolutely inappropriate, and that it is difficult to reconcile realistic dynamic range with other requirements.
I’d sidestep the issue like this: The cockpit view is not really what you see outside in space. It is a 3‑D rendering that is provided for you by the ship’s computer, based on sensor data, or at least some kind of AR. This is entirely plausible given future technology. With this explanation you could get away with arbitrary non-photorealistic rendering. And the ships don’t even need to have fragile glass windows any more.
Physically Based Shading
One of the current buzzwords in the graphics community is the term ‘physically based rendering’ or alternatively ‘physically based shading’ (PBS). While this term seems to imply that all aspects of rendering are physically correct (which they obviously will never be), this is not the meaning of it. Rather, PBS stands for a specific improvement over traditional surface shading that usually includes the following bullet points (for a non-technical explanation of these, see these slides):
- Linear lighting
- Energy conserving (’normalized’) specular highlights with varying glossiness
- Capability to differentiate between metals + dielectrics
- Fresnel effect
Based on what I could judge by just eyeballing Elite Dangerous, I’d confirm at least the first three, and maybe a Fresnel effect on water surfaces (but nowhere else).
The third screen shows the surface of a “Dreadnought” capital ship, in backlight. See this video to get an idea of how the entire ship looks like. Most of the surface is metallic and colorless, it’s the light from the central star that paints everything yellow. Glossiness is easy to estimate in motion, but not so easy in a static screenshot, so I have highlighted exemplars of high glossiness with blue marks and low glossiness with green marks. The shading behavior of these looks like they follow a normalization curve: the peak is either narrow and high, or broad and shallow. Taken together, this part of PBS is implemented textbook-perfect.
However, all metallic parts show a significant amount of diffuse reflection, while they should have none. I guess this was an artistic decision, because in space, there is not enough interesting environment to be reflected by an environment map or similar technique, it’s all black out there! So it looks like they gave all surfaces, including the metallic ones, at least some 10% diffuse or something to mitigate the black environment.
 Linear lighting can be measured with an experiment. Above is another screen shot from inside the Dreadnought. The region A is lit by my ship’s lights, the region B is in sunlight and the region C is lit by both light sources. If lighting is anywhere near linear, then the RGB color of C should equal the sum of the RGB colors of A and B, after gamma expansion. Just by eyeballing it feels like they do the right thing (for instance, the region C should not saturate), and some puny measurements seem to confirm this [6].
Linear lighting can be measured with an experiment. Above is another screen shot from inside the Dreadnought. The region A is lit by my ship’s lights, the region B is in sunlight and the region C is lit by both light sources. If lighting is anywhere near linear, then the RGB color of C should equal the sum of the RGB colors of A and B, after gamma expansion. Just by eyeballing it feels like they do the right thing (for instance, the region C should not saturate), and some puny measurements seem to confirm this [6].
The last ‘bullet point’ on the PBS list is the Fresnel effect, or the observation that reflectivity increases in the limit of a grazing angle. This effect seems to be intentionally absent in Elite Dangerous. It was surprisingly difficult to test because I had to find a non-metallic surface that the game allows you to sufficiently move the viewpoint against to get into a grazing angle. This basically rules out all lighting inside the cockpit, stations and capital ships.

I finally found this to be possible with respect to specular reflection in the ocean of a planet. So I embarked on a journey with the aforementioned super-cruise drive to try to get to the perfect angle. If the game gave me one credit for every time I got interdicted by pirates or police along the way, I could finally afford a Cobra Mk III … well, no not really, but I think there were a dozen interdictions over the course of one circumnavigation, which I think is a bit overdone.
See on the fifth screen shot a comparison of ocean appearance from different angles, with ED in the top row and the real ISS photos in the bottom row. In reality, the reflectivity of water at normal incidence is about 3%, and approaches 100% for grazing incidence. In ED, the effect exists (the highlight is definitely brighter at grazing incidence), but it is very weak.
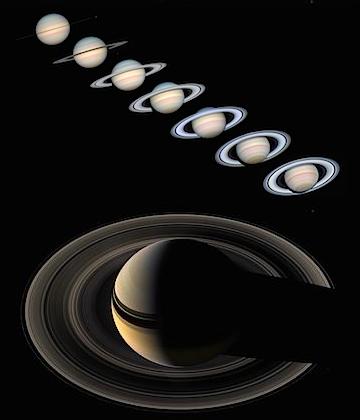 Planetary Rings and their Phase Curves
Planetary Rings and their Phase Curves
Above you can see how the relative brightness of different parts of Saturn’s rings varies with inclination and phase angle. This is to be expected, since a ring as a cloud of particles exhibits strong view-dependent occlusion and masking effects. Different parts of the ring have different optical thickness and albedo values, which results in different behavior under different light and view angles. For instance, the middle part of the ring, which appears brightest when Saturn is in opposition becomes the darkest part when seen in backlight. These subtle shading variations are not only of theoretical interest. Elite Dangerous allows the player to approach a ring to the point where the discrete particles are resolved, which is a very cool feature and I find it well executed, overall. However there is almost always a shading mismatch between the different levels of detail (marked 1 to 4).

Elite Dangerous is not alone in this regard; shading mismatch between LODs is one of the Great Plagues of game rendering that is difficult to get right, so I don’t criticize here. I want to use this opportunity however to draw attention one more time to the Lommel-Seeliger BRDF (I mentioned that in a previous post, here), that, in the version for finite thickness, was specifically designed to model the appearance of Saturn’s rings. It still misses some important effects such as the opposition surge, but it should be an improvement over completely view-independent shading.
Closing Remarks
Many parts of this article were written against the first release of the Premium Beta, which was in June, but the shading has fundamentally remained the same throughout the releases, so this article reflects current state. However, ED is progressing at a steady pace, so I am looking forward to the next releases!
Appendix
These are the calculations to back up the arguments in the text. If you think there is an error, drop me a line or write a comment!
[1] Calculate the irradiance received at 12.76 light seconds distance to Theta Boötis. The formula for the irradiance received by a spherical light source with known radiance was already discussed on this page, and is
![]()
The values for the variables are listed in the table below. I use the 4‑th power law ![]() to estimate the radiance
to estimate the radiance ![]() from the known radiance of the sun
from the known radiance of the sun ![]() and the ratio of temperatures.
and the ratio of temperatures.
Surface temperature Surface radiance Radius Distance
The result is
![]()
[2] Calculate the time to heat one ton of iron by 2500 K.
Specific heat capacity Mass Temperature change Total amount of heat needed
Given the irradiance from above, assuming a cross sectional area of one square meter and that all radiation is absorbed, the time needed is
![]()
[3] Calculate the radiance ![]() of the pixel at point A. First, calculate the irradiance
of the pixel at point A. First, calculate the irradiance ![]() received at this distance from the central star, like we did in [1], but also account for the incidence angle. This star does not have a convenient Wikipedia page so I looked for individual references.
received at this distance from the central star, like we did in [1], but also account for the incidence angle. This star does not have a convenient Wikipedia page so I looked for individual references.
Star temperature (ref)
Star radiance Star radius (ref)
Distance Irradiance at normal incidence Irradiance at 50° incidence Side note: an insolation of 1600 watts per square meter is a little bit on the hot side, but could be habitable. However the planet would most likely not have large ice sheets under these conditions. For comparison, the earth gets 1367 W/m² from our sun. (Edit 2021: The above simple calculation ignores the limb-darkening effect so that the true insolation is probably closer to the value on earth.)
In the second step, calculate the reflected radiance ![]() from
from ![]() , assuming the most simple Lambertian BRDF and somewhat guessing the albedo of the surface.
, assuming the most simple Lambertian BRDF and somewhat guessing the albedo of the surface.
Albedo of snow-ice (possibly dirty) Lambertian BRDF
Plugging in the values yields
![]()
[4] Calculate the radiance ![]() of the pixel representing the selected system at point B. The first step is again to calculate the irradiance
of the pixel representing the selected system at point B. The first step is again to calculate the irradiance ![]() . To keep the calculation simple, we lump together the contributions of the 3 stars of this system into a single radiant intensity
. To keep the calculation simple, we lump together the contributions of the 3 stars of this system into a single radiant intensity ![]() , which is stated as 2.2 times that of our sun.
, which is stated as 2.2 times that of our sun.
Radiant intensity Distance Irradiance
The next step is to assume that ![]() comes from a light source with the size of a single pixel. The formula for this is the reverse of [1] together with the substitution
comes from a light source with the size of a single pixel. The formula for this is the reverse of [1] together with the substitution ![]() :
:
![]()
where ![]() is now the apparent radius of a single pixel. For the center of the screen projection this is given by
is now the apparent radius of a single pixel. For the center of the screen projection this is given by
![]()
My screen resolution was 1600 × 900 and the FOV slider was at maximum. Based on a simple timing experiment with my ship turning I think the FOV is exactly 90° in this case.
Horizontal field of view Horizontal screen resolution Apparent pixel radius
Plugging in the values yields
![]()
and the EV difference is
![]()
Side note: Yes, this means the EV difference is resolution dependent. The brightness of star pixels increases with resolution. In the extreme case, when the resolution is so high that the star is resolved, it would have to approach the star’s actual surface radiance.
[5] Calculate the RGB value for the star pixel based on the reference color #BFA575. The simplest model of a computer display is a power law, characterized by its gamma value:
![]()
The highest component of the reference color is hexadecimal #BF, which is 191 in decimal. We use the commonplace gamma value of 2.2.
Reference RGB value Display gamma
resulting in
![]()
or rounded up to #030303 as grey color.
[6] Check the hypothesis that the colors were added linearly (ie. after gamma expansion). From a downsized screenshot we take RGB samples at locations A, B and C, expressed as percentage value. These values are gamma expanded via
![]()
with ![]() taken as a common value for display gamma. The values in the third and fourth rows are in better agreement on the right (‘linear’) column than on the left. On a side node, the values in the left column show how lighting would have clipped if the RGB values are added naively.
taken as a common value for display gamma. The values in the third and fourth rows are in better agreement on the right (‘linear’) column than on the left. On a side node, the values in the left column show how lighting would have clipped if the RGB values are added naively.
Location SampleD RGB Linear RGB A 0.45 0.45 0.57 0.17 0.17 0.29 B 0.68 0.55 0.35 0.43 0.27 0.10 C 0.80 0.71 0.69 0.61 0.47 0.43 A+B 1.31 1.00 0.92 0.60 0.44 0.39


Nice post, I like the lighting effects in elite dangerous, even if they are not perhaps realistic, it has a good artistic/futuristic quality.
Pingback: So, where are the stars? | The Tenth Planet
Pingback: Who’s Out There?: Elite Dangerous & the Space Race | wreckreation.org
Pingback: Caveat: Even NASA pictures may not be linear (or the wrong kind of linear) | The Tenth Planet