Followup: Normal Mapping Without Precomputed Tangents

Veröffentlicht am 20.01.2013 von christian

This post is a follow-up to my 2006 ShaderX⁵ article [4] about normal mapping without a pre-computed tangent basis. In the time since then I have refined this technique with lessons learned in real life. For those unfamiliar with the topic, the motivation was to construct the tangent frame on the fly in the pixel shader, which ironically is the exact opposite of the motivation from [2]:

Since it is not 1997 anymore, doing the tangent space on-the-fly has some potential benefits, such as reduced complexity of asset tools, per-vertex bandwidth and storage, attribute interpolators, transform work for skinned meshes and last but not least, the possibility to apply normal maps to any procedurally generated texture coordinates or non-linear deformations.

Intermission: Tangents vs Cotangents

The way that normal mapping is traditionally defined is, as I think, flawed, and I would like to point this out with a simple C++ metaphor. Suppose we had a class for vectors, for example called Vector3, but we also had a different class for covectors, called Covector3. The latter would be a clone of the ordinary vector class, except that it behaves differently under a transformation (Edit 2018: see this article for a comprehensive introduction to the theory behind covectors and dual spaces). As you may know, normal vectors are an example of such covectors, so we’re going to declare them as such. Now imagine the following function:

Vector3 tangent;
Vector3 bitangent;
Covector3 normal;
 
Covector3 perturb_normal( float a, float b, float c )
{
    return a * tangent +
           b * bitangent + 
           c * normal; 
           // ^^^^ compile-error: type mismatch for operator +
}

The above function mixes vectors and covectors in a single expression, which in this fictional example leads to a type mismatch error. If the normal is of type Covector3, then the tangent and the bitangent should be too, otherwise they cannot form a consistent frame, can they? In real life shader code of course, everything would be defined as float3 and be fine, or rather not.

Mathematical Compile Error

Unfortunately, the above mismatch is exactly how the ‘tangent frame’ for the purpose of normal mapping was introduced by the authors of [2]. This type mismatch is invisible as long as the tangent frame is orthogonal. When the exercise is however to reconstruct the tangent frame in the pixel shader, as this article is about, then we have to deal with a non-orthogonal screen projection. This is the reason why in the book I had introduced both $\vec{T}$ (which should be called co-tangent) and $\vec{B}$ (now it gets somewhat silly, it should be called co-bi-tangent) as covectors, otherwise the algorithm does not work. I have to admit that I could have been more articulate about this detail. This has caused real confusion, cf from gamedev.net:

The discrepancy is explained above, as my ‘tangent vectors’ are really covectors. The definition on page 132 is consistent with that of a covector, and so the frame $\left(\vec{T}|\vec{B}|\vec{N}\right)$ should be called a cotangent frame.

Intermission 2: Blinns Perturbed Normals (History Channel)

In this section I would like to show how the definition of $\vec{T}$ and $\vec{B}$ as covectors follows naturally from Blinn’s original bump mapping paper [1]. Blinn considers a curved parametric surface, for instance, a Bezier-patch, on which he defines tangent vectors $\vec{p}_u$ and $\vec{p}_v$ as the derivatives of the position $\vec{p}$ with respect to $u$ and $v$ .

In this context it is a convention to use subscripts as a shorthand for partial derivatives, so he is really saying $\vec{p}_u = {\partial\vec{p} \over \partial u}$ , etc. He also introduces the surface normal $\vec{N} = \vec{p}_u \times \vec{p}_v$ and a bump height function $f$ , which is used to displace the surface. In the end, he arrives at a formula for a first order approximation of the perturbed normal:

$\vec{N}' \simeq \vec{N} + \frac{f_u \vec{N} \times \vec{p}_v + f_v \vec{p}_u \times \vec{N}}{|\vec{N}|} ,$

I would like to draw your attention towards the terms $\vec{N} \times \vec{p}_v$ and $\vec{p}_u \times \vec{N}$ . They are the perpendiculars to $\vec{p}_u$ and $\vec{p}_v$ in the tangent plane, and together form a vector basis for the displacements $f_u$ and $f_v$ . They are also covectors (this is easy to verify as they behave like covectors under transformation) so adding them to the normal does not raise said type mismatch. If we divide these terms one more time by $|\vec{N}|$ and flip their signs, we’ll arrive at the ShaderX⁵ definition of $\vec{T}$ and $\vec{B}$ as follows:

$\begin{align*} \vec{T} &= -\frac{\vec{N} \times \vec{p}_v}{|\vec{N}|^2} = \nabla u, & \vec{B} &= -\frac{\vec{p}_u \times \vec{N}}{|\vec{N}|^2} = \nabla v, \end{align*}$

$\vec{N}' \simeq \hat{N} - f_u \vec{T} - f_v \vec{B} ,$

where the hat (as in $\hat{N}$ ) denotes the normalized normal. $\vec{T}$ can be interpreted as the normal to the plane of constant $u$ , and likewise $\vec{B}$ as the normal to the plane of constant $v$ . Therefore we have three normal vectors, or covectors, $\vec{T}$ , $\vec{B}$ and $\vec{N}$ , and they are the a basis of a cotangent frame. Equivalently, $\vec{T}$ and $\vec{B}$ are the gradients of $u$ and $v$ , which is the definition I had used in the book. The magnitude of the gradient therefore determines the bump strength, a fact that I will discuss later when it comes to scale invariance.

A Little Unlearning

The mistake of many authors is to unwittingly take $\vec{T}$ and $\vec{B}$ for $\vec{p}_u$ and $\vec{p}_v$ , which only works as long as the vectors are orthogonal. Let’s unlearn ‘tangent’, relearn ‘cotangent’, and repeat the historical development from this perspective: Peercy et al. [2] precomputes the values $f_u$ and $f_v$ (the change of bump height per change of texture coordinate) and stores them in a texture. They call it ’normal map’, but is a really something like a ’slope map’, and they have been reinvented recently under the name of derivative maps. Such a slope map cannot represent horizontal normals, as this would need an infinite slope to do so. It also needs some ‘bump scale factor’ stored somewhere as meta data. Kilgard [3] introduces the modern concept of a normal map as an encoded rotation operator, which does away with the approximation altogether, and instead goes to define the perturbed normal directly as

$\vec{N}' = a \vec{T} + b \vec{B} + c \hat{N} ,$

where the coefficients $a$ , $b$ and $c$ are read from a texture. Most people would think that a normal map stores normals, but this is only superficially true. The idea of Kilgard was, since the unperturbed normal has coordinates $(0,0,1)$ , it is sufficient to store the last column of the rotation matrix that would rotate the unperturbed normal to its perturbed position. So yes, a normal map stores basis vectors that correspond to perturbed normals, but it really is an encoded rotation operator. The difficulty starts to show up when normal maps are blended, since this is then an interpolation of rotation operators, with all the complexity that goes with it (for an excellent review, see the article about Reoriented Normal Mapping [5] here).

Solution of the Cotangent Frame

The problem to be solved for our purpose is the opposite as that of Blinn, the perturbed normal is known (from the normal map), but the cotangent frame is unknown. I’ll give a short revision of how I originally solved it. Define the unknown cotangents $\vec{T} = \nabla u$ and $\vec{B} = \nabla v$ as the gradients of the texture coordinates $u$ and $v$ as functions of position $\vec{p}$ , such that

$\begin{align*} \mathrm{d} u &= \vec{T} \cdot \mathrm{d} \vec{p} , & \mathrm{d} v &= \vec{B} \cdot \mathrm{d} \vec{p} , \end{align*}$

where $\cdot$ is the dot product. The gradients are constant over the surface of an interpolated triangle, so introduce the edge differences $\Delta u_{1,2}$ , $\Delta v_{1,2}$ and $\Delta \vec{p_{1,2}}$ . The unknown cotangents have to satisfy the constraints

$\begin{align*} \Delta u_1 &= \vec{T} \cdot \Delta \vec{p_1} , & \Delta v_1 &= \vec{B} \cdot \Delta \vec{p_1} , \\ \Delta u_2 &= \vec{T} \cdot \Delta \vec{p_2} , & \Delta v_2 &= \vec{B} \cdot \Delta \vec{p_2} , \\ 0 &= \vec{T} \cdot \Delta \vec{p_1} \times \Delta \vec{p_2} , & 0 &= \vec{B} \cdot \Delta \vec{p_1} \times \Delta \vec{p_2} , \end{align*}$

where $\times$ is the cross product. The first two rows follow from the definition, and the last row ensures that $\vec{T}$ and $\vec{B}$ have no component in the direction of the normal. The last row is needed otherwise the problem is underdetermined. It is straightforward then to express the solution in matrix form. For $\vec{T}$ ,

$\vec{T} = \begin{pmatrix} \Delta \vec{p_1} \\ \Delta \vec{p_2} \\ \Delta \vec{p_1} \times \Delta \vec{p_2} \end{pmatrix}^{-1} \begin{pmatrix} \Delta u_1 \\ \Delta u_2 \\ 0 \end{pmatrix} ,$

and analogously for $\vec{B}$ with $\Delta v$ .

Into the Shader Code

The above result looks daunting, as it calls for a matrix inverse in every pixel in order to compute the cotangent frame! However, many symmetries can be exploited to make that almost disappear. Below is an example of a function written in GLSL to calculate the inverse of a 3×3 matrix. A similar function written in HLSL appeared in the book, and then I tried to optimize the hell out of it. Forget this approach as we are not going to need it at all. Just observe how the adjugate and the determinant can be made from cross products:

mat3 inverse3x3( mat3 M )
{
    // The original was written in HLSL, but this is GLSL, 
    // therefore
    // - the array index selects columns, so M_t[0] is the 
    //   first row of M, etc.
    // - the mat3 constructor assembles columns, so 
    //   cross( M_t[1], M_t[2] ) becomes the first column
    //   of the adjugate, etc.
    // - for the determinant, it does not matter whether it is
    //   computed with M or with M_t; but using M_t makes it
    //   easier to follow the derivation in the text
    mat3 M_t = transpose( M ); 
    float det = dot( cross( M_t[0], M_t[1] ), M_t[2] );
    mat3 adjugate = mat3( cross( M_t[1], M_t[2] ),
                          cross( M_t[2], M_t[0] ),
                          cross( M_t[0], M_t[1] ) );
    return adjugate / det;
}

We can substitute the rows of the matrix from above into the code, then expand and simplify. This procedure results in a new expression for $\vec{T}$ . The determinant becomes $\left| \Delta \vec{p_1} \times \Delta \vec{p_2} \right|^2$ , and the adjugate can be written in terms of two new expressions, let’s call them $\Delta \vec{p_1}_\perp$ and $\Delta \vec{p_2}_\perp$ (with $\perp$ read as ‘perp’), which becomes

$\vec{T} = \frac{1}{\left| \Delta \vec{p_1} \times \Delta \vec{p_2} \right|^2} \begin{pmatrix} \Delta \vec{p_2}_\perp \\ \Delta \vec{p_1}_\perp \\ \Delta \vec{p_1} \times \Delta \vec{p_2} \end{pmatrix}^\mathrm{T} \begin{pmatrix} \Delta u_1 \\ \Delta u_2 \\ 0 \end{pmatrix} ,$

$\begin{align*} \Delta \vec{p_2}_\perp &= \Delta \vec{p_2} \times \left( \Delta \vec{p_1} \times \Delta \vec{p_2} \right) , \\ \Delta \vec{p_1}_\perp &= \left( \Delta \vec{p_1} \times \Delta \vec{p_2} \right) \times \Delta \vec{p_1} . \end{align*}$

As you might guessed it, $\Delta \vec{p_1}_\perp$ and $\Delta \vec{p_2}_\perp$ are the perpendiculars to the triangle edges in the triangle plane. Say Hello! They are, again, covectors and form a proper basis for cotangent space. To simplify things further, observe:

The last row of the matrix is irrelevant since it is multiplied with zero.
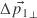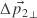The other matrix rows contain the perpendiculars ( $\Delta \vec{p_1}_\perp$ and $\Delta \vec{p_2}_\perp$ ), which after transposition just multiply with the texture edge differences.
The perpendiculars can use the interpolated vertex normal 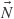$\vec{N}$ instead of the face normal $\Delta \vec{p_1} \times \Delta \vec{p_2}$ , which is simpler and looks even nicer.
The determinant (the expression 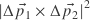$\left| \Delta \vec{p_1} \times \Delta \vec{p_2} \right|^2$ ) can be handled in a special way, which is explained below in the section about scale invariance.

Taken together, the optimized code is shown below, which is even simpler than the one I had originally published, and yet higher quality:

mat3 cotangent_frame( vec3 N, vec3 p, vec2 uv )
{
    // get edge vectors of the pixel triangle
    vec3 dp1 = dFdx( p );
    vec3 dp2 = dFdy( p );
    vec2 duv1 = dFdx( uv );
    vec2 duv2 = dFdy( uv );
 
    // solve the linear system
    vec3 dp2perp = cross( dp2, N );
    vec3 dp1perp = cross( N, dp1 );
    vec3 T = dp2perp * duv1.x + dp1perp * duv2.x;
    vec3 B = dp2perp * duv1.y + dp1perp * duv2.y;
 
    // construct a scale-invariant frame 
    float invmax = inversesqrt( max( dot(T,T), dot(B,B) ) );
    return mat3( T * invmax, B * invmax, N );
}

Scale invariance

The determinant $\left| \Delta \vec{p_1} \times \Delta \vec{p_2} \right|^2$ was left over as a scale factor in the above expression. This has the consequence that the resulting cotangents $\vec{T}$ and $\vec{B}$ are not scale invariant, but will vary inversely with the scale of the geometry. It is the natural consequence of them being gradients. If the scale of the geomtery increases, and everything else is left unchanged, then the change of texture coordinate per unit change of position gets smaller, which reduces $\vec{T} = \nabla u = \left( \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z} \right)$ and similarly $\vec{B}$ in relation to $\vec{N}$ . The effect of all this is a diminished pertubation of the normal when the scale of the geometry is increased, as if a heightfield was stretched.

Obviously this behavior, while totally logical and correct, would limit the usefulness of normal maps to be applied on different scale geometry. My solution was and still is to ignore the determinant and just normalize $\vec{T}$ and $\vec{B}$ to whichever of them is largest, as seen in the code. This solution preserves the relative lengths of $\vec{T}$ and $\vec{B}$ , so that a skewed or stretched cotangent space is sill handled correctly, while having an overall scale invariance.

Non-perspective optimization

As the ultimate optimization, I also considered what happens when we can assume $\Delta \vec{p_1} = \Delta \vec{p_2}_\perp$ and $\Delta \vec{p_2} = \Delta \vec{p_1}_\perp$ . This means we have a right triangle and the perpendiculars fall on the triangle edges. In the pixel shader, this condition is true whenever the screen-projection of the surface is without perspective distortion. There is a nice figure demonstrating this fact in [4]. This optimization saves another two cross products, but in my opinion, the quality suffers heavily should there actually be a perspective distortion.

Putting it together

To make the post complete, I’ll show how the cotangent frame is actually used to perturb the interpolated vertex normal. The function perturb_normal does just that, using the backwards view vector for the vertex position (this is ok because only differences matter, and the eye position goes away in the difference as it is constant).

vec3 perturb_normal( vec3 N, vec3 V, vec2 texcoord )
{
    // assume N, the interpolated vertex normal and 
    // V, the view vector (vertex to eye)
    vec3 map = texture2D( mapBump, texcoord ).xyz;
#ifdef WITH_NORMALMAP_UNSIGNED
    map = map * 255./127. - 128./127.;
#endif
#ifdef WITH_NORMALMAP_2CHANNEL
    map.z = sqrt( 1. - dot( map.xy, map.xy ) );
#endif
#ifdef WITH_NORMALMAP_GREEN_UP
    map.y = -map.y;
#endif
    mat3 TBN = cotangent_frame( N, -V, texcoord );
    return normalize( TBN * map );
}

varying vec3 g_vertexnormal;
varying	vec3 g_viewvector;  // camera pos - vertex pos
varying vec2 g_texcoord;
 
void main()
{
    vec3 N = normalize( g_vertexnormal );
 
#ifdef WITH_NORMALMAP
    N = perturb_normal( N, g_viewvector, g_texcoord );
#endif
 
    // ...
}

The green axis

Both OpenGL and DirectX place the texture coordinate origin at the start of the image pixel data. The texture coordinate (0,0) is in the corner of the pixel where the image data pointer points to. Contrast this to most 3‑D modeling packages that place the texture coordinate origin at the lower left corner in the uv-unwrap view. Unless the image format is bottom-up, this means the texture coordinate origin is in the corner of the first pixel of the last image row. Quite a difference!
An image search on Google reveals that there is no dominant convention for the green channel in normal maps. Some have green pointing up and some have green pointing down. My artists prefer green pointing up for two reasons: It’s the format that 3ds Max expects for rendering, and it supposedly looks more natural with the ‘green illumination from above’, so this helps with eyeballing normal maps.

Sign Expansion

The sign expansion deserves a little elaboration because I try to use signed texture formats whenever possible. With the unsigned format, the value ½ cannot be represented exactly (it’s between 127 and 128). The signed format does not have this problem, but in exchange, has an ambiguous encoding for −1 (can be either −127 or −128). If the hardware is incapable of signed texture formats, I want to be able to pass it as an unsigned format and emulate the exact sign expansion in the shader. This is the origin of the seemingly odd values in the sign expansion.

In Hindsight

The original article in ShaderX⁵ was written as a proof-of-concept. Although the algorithm was tested and worked, it was a little expensive for that time. Fast forward to today and the picture has changed. I am now employing this algorithm in real-life projects for great benefit. I no longer bother with tangents as vertex attributes and all the associated complexity. For example, I don’t care whether the COLLADA exporter of Max or Maya (yes I’m relying on COLLADA these days) output usable tangents for skinned meshes, nor do I bother to import them, because I don’t need them! For the artists, it doesn’t occur to them that an aspect of the asset pipeline is missing, because It’s all natural: There is a geometry, there are texture coordinates and there is a normal map, and just works.

Take Away

There are no ‘tangent frames’ when it comes to normal mapping. A tangent frame which includes the normal is logically ill-formed. All there is are cotangent frames in disguise when the frame is orthogonal. When the frame is not orthogonal, then tangent frames will stop working. Use cotangent frames instead.

References

[1] James Blinn, “Simulation of wrinkled surfaces”, SIGGRAPH 1978
http://research.microsoft.com/pubs/73939/p286-blinn.pdf

[2] Mark Peercy, John Airey, Brian Cabral, “Efficient Bump Mapping Hardware”, SIGGRAPH 1997
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.42.4736

[3] Mark J Kilgard, “A Practical and Robust Bump-mapping Technique for Today’s GPUs”, GDC 2000
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.18.537

[4] Christian Schüler, “Normal Mapping without Precomputed Tangents”, ShaderX 5, Chapter 2.6, pp. 131 – 140

[5] Colin Barré-Brisebois and Stephen Hill, “Blending in Detail”,
http://blog.selfshadow.com/publications/blending-in-detail/

111 Gedanken zu „Followup: Normal Mapping Without Precomputed Tangents“

Michael sagte am 08.02.2014 um 20:41 Uhr :

Excellent! Thank you so much for taking the time to answer my questions. I had started to suspect that the inverse-transpose of the Pu|Pv|N matrix was a roundabout way of computing what you compute directly, and I’m very glad to hear that’s the case. I still have some learning to do to comfortably manipulate covectors, but it helps a great deal that the end result is something I recognize…and understanding covectors more thoroughly will finally take the “black magic” out of why the inverse-transpose of Pu|Pv|N also works (much less efficiently of course).

Antworten ↓
Pingback: Spellforce 2 Demons of the Past | The Tenth Planet
Pingback: Decals (deferred rendering) | IceFall Games
Pingback: Balancing | Spellcaster Studios
Ana sagte am 13.08.2014 um 04:50 Uhr :

Hi there! I’m having trouble using the functions dFdx() and dFdy()… tried adding this line:
#extension GL_OES_standard_derivatives : enable
in my shader, but it gives me the message that the extension isn’t supported. Do you have any idea about how i’m supposed to do this?

Antworten ↓
- christian sagte am 15.08.2014 um 19:06 Uhr :
  
  Hi Ana, according to http://www.khronos.org/registry/gles/extensions/OES/OES_standard_derivatives.txt
  You’re on the right track, but if it says the extension is not supported then it looks like these are not supported by your hardware … .)
Sherry sagte am 07.09.2014 um 19:45 Uhr :

Hi Christian,
I’m researching on the run-time generate tbn matrix related topics recently, and I found your article very interesting. I’m wondering if I want to integrate your glsl shader with my code, which is written in directx/hlsl, should I use the ‑N instead in the final result of cotangent frame matrix?(for dealing with the Right-handed and left-handed issue). If this is not the solution, what should I do? Thanks.

Antworten ↓
- christian sagte am 08.09.2014 um 08:13 Uhr :
  
  Hi Sherry
  the one gotcha you need to be aware of is that HLSL’s ddy has different sign than dFdy, due to OpenGL’s window coordinates being bottom-to-top (when not rendering into an FBO, that is). Other than that, it is just syntactical code conversion. For testing, you can substitute N with the face normal generated by crossing dp1 and dp2; that must work in every case, whatever sign convention the screen space derivatives have.
Andrzej sagte am 28.10.2014 um 14:46 Uhr :

Hi Christian!
First, thanks for an explanatory article, it’s great!
I still have a couple of questions. Lets list some facts:
a) You said in response to Michael that transpose(TBN) can be used to transform eg. V vector from world-space to tangent-space.
b) dFdx and dFdy, and chence dp1/2 and duv1/2 are constant over a triangle.
Based on that facts, can your TBN be computed in geometry-shader on per-triangle basis, and its transpose used to transform V, L, Blinn’s half vector, etc. to tangent-space, in order to make “classic” lightning in pixel-shader?
I’ve found something similar in: http://www.slideshare.net/Mark_Kilgard/geometryshaderbasedbumpmappingsetup
but there is nothing about common tangent-basis calculation in texture baking tool and shader. The latter is neccesary, since substituting normal map with flat normal-map (to get simple lightning) produces faceted look, as in Kilgard’s approach. The second question: do you have a plugin for xNormal, which can compute correct per-triangle tangent basis?

Antworten ↓
- christian sagte am 30.10.2014 um 05:54 Uhr :
  
  Hi Andrzej,
  yes, you can (and I have) do the same calculations in the geometry shader. The cotangent basis is always computed from a triangle. In the pixel shader, the ‘triangle’ is implicitly spanned between the current pixel and neighboring pixels. In the geometry shader, you use the actual triangle, i.e., dFdx and dFdy are substituted with the actual edge differences. The rest will be identical.
  You can then pass TBN down to the pixel shader, or use it to transform other quantities and pass these.
  
  Faceting: As I said before, the T and B vectors will be faceted, but the N vector can use the interpolated normal to give a smoother look. In practice, if the UV mapping does not stray too far from the square patch assumption, the faceting will be unnoticeable.
Andrzej sagte am 31.10.2014 um 22:40 Uhr :

Thank You very much, Christian!

I implemented the technique and wrote XNormal plugin, yet, when transforming generated tangent-space normal map back to object-space (by XNormal tool), I didn’t get the expected result. I’ll try to make per-triangle tbn computation order-independent and check the code.

Antworten ↓
Cormac Guerin sagte am 13.04.2015 um 06:49 Uhr :

Really nice post, I’m working on some terrain at the moment for a poject in my spare time.. I came accross your site yesterday while looking for an in shader bumpmapping technique and Imlemented it right away
I really like the results and performance also seems good.. but I was wondering about applying such techniques to large scenes, I don’t need the shader applied to certain regions(black/very dark places).. But my understanding is that it will be applied to ever pixel on the terrain regardless of whether I want it lit or not..
This is a bit off topic so apologies for that, but in terms on optimization, if applied to a black region would glsl avoid processing that or do you have any recommendations for performance tweaking, conditionals/branching etc.. I understand a stencil buffer could assist here, but these type of optimizations are really interesting, it could make a good post in it’s own right.
Thanks again for your insightful article!

Antworten ↓
- christian sagte am 13.04.2015 um 14:36 Uhr :
  
  Hi Cormac,
  since the work is done per pixel, the performance doesn’t depend on the size of the scene, but only on the number of rendered pixels. This is a nice property which is called “output-sensitivity”, ie. the performance depends on the size of the output, not the size of the input. For large scenes, you want all rendering to be output sensitive, so you do occlusion culling and the like.
  Branching optimizations only pay off if the amount of work that is avoided is large, for instance, when skipping over a large number of shadow map samples. In my experience, the tangent space calculation described here (essentially on the order of 10 to 20 shader instructions) is not worth the cost of a branch. But if in doubt, just profile it!
Cormac sagte am 16.04.2015 um 07:53 Uhr :

Thanks Christian !!
The performance is actually surprisingly good.. The card I’m running on is quite old and FPS drop is not significant which is impressive.
It’s funny when I applied it to my scene I started getting some strange arifacts in the normals. I didn’t have time too dig into it yet, perhap my axes are mixed up or something, I’ll check it again tonight.

https://drive.google.com/folderview?id=0B9yRwnwRzOCnZjFDVFdScDV6Y3M&usp=sharing

Antworten ↓
- christian sagte am 16.04.2015 um 13:38 Uhr :
  
  If you mean the seams that appear at triangle borders, these are related to the fact that dFdx/dFdy of the texture coordinate is constant across a triangle, so there will be a discontinuous change in the two tangent vectors when the direction of the texture mapping changes. This is expected behavior, especially if the texture mapping is sheared/stretched, as is usually the case on a procedural terrain. The lighting will be/should be correct.
Andrzej sagte am 23.05.2015 um 22:38 Uhr :

Hi Christian!
I thought about seams and lightning discontinuities and have another couple of questions in this area. But first some facts.
1. When we consider a texture with normals in object space there are almost no seams; distortions are mostly related to nonexact interpolation over an edge in a mesh, whose sides are unconnected in the texture (eg. due to different lenght, angles, etc.)
2. No matter how a tangent space is defined (per-pixel with T,B and N interpolated over triangle, with only N interpolated, or even constant TBN over triangle), tangent-space normals should always decode to object-space counterparts.

Why it isn’t the case in Your method? I think its because triangles adjacent in a mesh are also adjacent in texture-space. Then, when rendering an edge, you read the normal from a texture, but you may ‘decode’ it with a wrong tangent-space basis — from the other side triangle (with p=0.5). Things get worse with linear texture sampler applied instead of point sampler. Note how the trick with ‘the same’ tangent-space on both sides of the edge works well in this situation.

So, the question: shoudn’t all triangles in a mesh be unconnected in the texture space for Your method to work? (It sholdn’t be a problem to code an additional ‘texture-breaker’ for a tool-chain.)

Antworten ↓
- christian sagte am 24.05.2015 um 18:09 Uhr :
  
  Hi Andrzej,
  have a look at the very first posts in this thread. There is a discussion about the difference between “painted normal maps” and “baked normal maps”.
  
  For painted normal maps, the method is in principle, correct. The lighting is always exactly faithful to the implied height map, the slope of which may change abruptly at a triangle border, depending on the UV mapping. That’s just how things are.
  
  For baked normal maps, where you want a result that looks the same as a high-poly geometry, the baking procedure would have to use the same TBN that is generated in the pixel shader, in order to match perfectly.
  This can be done, however due to texture interpolation, the discontinuity can only be approximated down to the texel level. So there would be slight mismatch within the texel that straddles the triangle boundary. If you want to eliminate even that, you need to pay 3 times the number of vertices to make the UV atlas for each triangle separate.
  
  In my practice, I really don’t care. We’re have been using what everyone else does: x‑normal, crazy bump, substance B2M, etc, and I have yet to receive a single ‘complaint’ from artists. :)
Andrzej sagte am 24.05.2015 um 21:43 Uhr :

Somehow I forgot that normal maps can also be painted :-)
Maybe separating triangles in the texture domain is unnecessary in practice, but as I am teaching about normal mapping, I want to know every aspect of it.

Thanks a lot!

Antworten ↓
Andrzej sagte am 09.06.2015 um 22:56 Uhr :

Christian, please help me with another issue. In many NM tutorials over the net, lightning is done in tangent space, i.e., Light and Blinn’s Half are transformed into tangent space at each vertex, to be interpolated over a triangle. Considering each TBN forms orthonormal basis, why this works only for L and not for H? It gives me strange artefacts, while interpolating ‘plain’ H and transforming it at each fragment by interpolated & normalized TBN works well (for simplicity, I consider world-space $\equiv$ object-space).

Antworten ↓
- christian sagte am 29.06.2015 um 17:53 Uhr :
  
  Hi Andrzej,
  there are some earlier comments on this issue. One of the salient points of the article is that the TBN frame is, in general, not orthonormal. Therefore, dot products are not preserved across transforms.
Andrzej sagte am 30.06.2015 um 20:44 Uhr :

Hi Christian,
Thanks! But in main case I do have orthonormal base at each vertex (N from model, T computed by mikkTSpace and orthogonalized by Gram-Schmit method, B as cross product). According to many tutorials this should work, yet in [2] they say this can be considered an approximation only. Who is right then? I don’t know if there is bug in my code or triangles in low poly model are too big for such approximation?

Antworten ↓
Anonymous sagte am 22.09.2015 um 15:23 Uhr :

If you like covectors, I guess you will like Geometric Algebra and Grassmann Algebra :-)

Antworten ↓
- christian sagte am 26.09.2015 um 00:21 Uhr :
  
  I do.
Pingback: mathematics – Tangent space – Lengyel vs ShaderX5 – difference | Asking
Peter sagte am 11.12.2015 um 21:57 Uhr :

Hi Christian,
Very fascinating article and it looks to be exactly what I was looking for. Unfortunately, I can’t seem to get this working in HLSL: I must be doing something really stupid but I can’t seem to figure it out. I’m doing my lighting calculations in view space but having read through the comments, it shouldn’t affect the calculations regardless?

Here’s the “port” of your code: http://pastebin.com/cDr1jnPb

Thanks!

Antworten ↓
- christian sagte am 30.06.2018 um 15:13 Uhr :
  
  Hi Peter,
  when translating from GLSL to HLSL you must observe two things:
  1. Matrix order (row- vs column major). The mat3(…) constructor in GLSL assembles the matrix column-wise.
  2. The dFdy and ddy have different sign, because the coordinate system in GL is bottom-to-top.
Pingback: WebGL techniques for normal mapping on morph targets? – Blog 5 Star
Pingback: Rendering Terrain Part 20 – Normal and Displacement Mapping – The Demon Throne
maval sagte am 23.11.2016 um 11:47 Uhr :

hi, l’d like to ask if this method can be used in the ward anisotropic lighting equation, which is using tangent and binormal directly.

I found the result to be facet because the tangent and binormal are facet, is that means I can’t use your method in this situation? sorry about my bad english..

Antworten ↓
- Indy Ray sagte am 08.02.2018 um 23:40 Uhr :
  
  Hey Maval,
  
  I just came across this same post when I was investigating the usage of computing our tangents in the fragment shader.
  
  Since T and B are faceted with this technique, it cannot be used with an anisotropic brdf, so long as the anisotropy depends on the tangent frame.
  
  I also do not think it’s possible to correct for this without additional information non-local from the triangle.
  
  Indy
- christian sagte am 30.06.2018 um 14:50 Uhr :
  
  Hi Maval,
  the faceting of the tangents is not very noticable in practice, so I would just give it a try and see what happens. It all depends on how strong the tangents are curved within the specific UV mapping at hand.
François Guthmann sagte am 19.08.2017 um 19:52 Uhr :

Wow thank you very much for this. I was supposed to implement normal mapping in my PBR renderer but couldn’t get over the fact that those co-tangent and bi-co-tangent were a huge pain in the back to transfer to the vertex shader (with much data duplicated). This is so much better, thank you :D.

Antworten ↓
- christian sagte am 30.06.2018 um 14:51 Uhr :
  
  Thank you.
Alexander sagte am 01.09.2017 um 12:51 Uhr :

Hi Christian. I was trying to produce similar formulas in a different way and somehow the result is different and does not work. As a challenge for myself I’m trying to find the error in my approach but can not.

As a basis of my approach do deduce gradient du/dp, I assume that both texture coordinates u and world-point p on the triangle are functions of screen coordinates (sx, sy). So to differentiate du(p(sx, sy))/dp(sx, sy) I use rule of partial derivatives:
du/dp = du/dsx * dsx/dp + du/dsy * dsy/dp. From here (du/dsx, du/dsy) is basically (duv1.x, duv2.x) in your code.

To compute dsx/dp, I try to inverse the derivatives: dsx/dp = 1 / (dsx/dp), which is equal to (1 / dFdx(p.x), 1 / dFdx(p.y), 1 / dFdx(p.z)), but somehow that does not work because the result is different from dp2perp in your code. Can you clarify why?

Antworten ↓
- christian sagte am 18.07.2018 um 23:27 Uhr :
  
  Your terms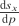 $\mathrm{d}s_x \over \mathrm{d}p$ and $\mathrm{d}s_y \over \mathrm{d}p$ are vector valued and together form a 2‑by‑3 Jacobian matrix, that contains the contribution of each component of the world space position to a change in screen coordinate.
  
  To get the inverse, you’d need to inverse that matrix, but you cannot do that because it’s not a square matrix. The problem is underdetermined. Augment the Jacobian with a virtual 3rd screen coordinate (the screen z coordinate, or depth coordinate) $\mathrm{d}s_z \over \mathrm{d}p$ to and equate that to zero, because it must stay constant for the solution to lie on the screen plane. Et voila, then you would have arrived at an exactly equivalent problem formulation as that which is described in the section ’solution to the co-tangent frame’.
Pingback: Followup: Normal Mapping Without Precomputed Tangents via @erkaman2 | hanecci's blog : はねっちブログ
Chuck Walbourn sagte am 12.12.2017 um 02:42 Uhr :

In my library, I have a debug shader that lets me visualize the normal, tangent, and (reconstructed) bi-tangent in the traditional “precomputed vertex tangents” scenario.

I’m trying to work out what the equivalent to the “per vertex tangent” is with a calculated TBN. The second and third row vectors don’t seem to match very closely with the original tangent/bi-tangent.

Antworten ↓
- Chuck Walbourn sagte am 12.12.2017 um 02:46 Uhr :
  
  Sorry, make that the first and second row vector. The third row vector is obviously the original per-vertex normal.
- christian sagte am 30.06.2018 um 14:56 Uhr :
  
  Hi Chuck,
  to get something that is like the traditional per-vertex tangent, you’d have to take the first two columns of the inverted matrix.
  
  The tangents and the co-tangents each answer different questions. The tangent answers what is the change in position with a change in uv. The co-tangents are normals to the planes of constant u and v, so they answer what direction is perpendicular to keeping uv constant. They’ll be equivalent as long as the tangent frame is orthogonal, but diverge when that is not the case.

The Tenth Planet

If it existed