This post is a follow-up to my 2006 ShaderX5 article [4] about normal mapping without a pre-computed tangent basis. In the time since then I have refined this technique with lessons learned in real life. For those unfamiliar with the topic, the motivation was to construct the tangent frame on the fly in the pixel shader, which ironically is the exact opposite of the motivation from [2]:

Since it is not 1997 anymore, doing the tangent space on-the-fly has some potential benefits, such as reduced complexity of asset tools, per-vertex bandwidth and storage, attribute interpolators, transform work for skinned meshes and last but not least, the possibility to apply normal maps to any procedurally generated texture coordinates or non-linear deformations.
Intermission: Tangents vs Cotangents
The way that normal mapping is traditionally defined is, as I think, flawed, and I would like to point this out with a simple C++ metaphor. Suppose we had a class for vectors, for example called Vector3, but we also had a different class for covectors, called Covector3. The latter would be a clone of the ordinary vector class, except that it behaves differently under a transformation (Edit 2018: see this article for a comprehensive introduction to the theory behind covectors and dual spaces). As you may know, normal vectors are an example of such covectors, so we’re going to declare them as such. Now imagine the following function:
Vector3 tangent; Vector3 bitangent; Covector3 normal; Covector3 perturb_normal( float a, float b, float c ) { return a * tangent + b * bitangent + c * normal; // ^^^^ compile-error: type mismatch for operator + } |
The above function mixes vectors and covectors in a single expression, which in this fictional example leads to a type mismatch error. If the normal is of type Covector3, then the tangent and the bitangent should be too, otherwise they cannot form a consistent frame, can they? In real life shader code of course, everything would be defined as float3 and be fine, or rather not.
Mathematical Compile Error
Unfortunately, the above mismatch is exactly how the ‘tangent frame’ for the purpose of normal mapping was introduced by the authors of [2]. This type mismatch is invisible as long as the tangent frame is orthogonal. When the exercise is however to reconstruct the tangent frame in the pixel shader, as this article is about, then we have to deal with a non-orthogonal screen projection. This is the reason why in the book I had introduced both ![]() (which should be called co-tangent) and
(which should be called co-tangent) and ![]() (now it gets somewhat silly, it should be called co-bi-tangent) as covectors, otherwise the algorithm does not work. I have to admit that I could have been more articulate about this detail. This has caused real confusion, cf from gamedev.net:
(now it gets somewhat silly, it should be called co-bi-tangent) as covectors, otherwise the algorithm does not work. I have to admit that I could have been more articulate about this detail. This has caused real confusion, cf from gamedev.net:

The discrepancy is explained above, as my ‘tangent vectors’ are really covectors. The definition on page 132 is consistent with that of a covector, and so the frame ![]() should be called a cotangent frame.
should be called a cotangent frame.
Intermission 2: Blinns Perturbed Normals (History Channel)
In this section I would like to show how the definition of ![]() and
and ![]() as covectors follows naturally from Blinn’s original bump mapping paper [1]. Blinn considers a curved parametric surface, for instance, a Bezier-patch, on which he defines tangent vectors
as covectors follows naturally from Blinn’s original bump mapping paper [1]. Blinn considers a curved parametric surface, for instance, a Bezier-patch, on which he defines tangent vectors ![]() and
and ![]() as the derivatives of the position
as the derivatives of the position ![]() with respect to
with respect to ![]() and
and ![]() .
.

In this context it is a convention to use subscripts as a shorthand for partial derivatives, so he is really saying ![]() , etc. He also introduces the surface normal
, etc. He also introduces the surface normal ![]() and a bump height function
and a bump height function ![]() , which is used to displace the surface. In the end, he arrives at a formula for a first order approximation of the perturbed normal:
, which is used to displace the surface. In the end, he arrives at a formula for a first order approximation of the perturbed normal:
![]()
I would like to draw your attention towards the terms ![]() and
and ![]() . They are the perpendiculars to
. They are the perpendiculars to ![]() and
and ![]() in the tangent plane, and together form a vector basis for the displacements
in the tangent plane, and together form a vector basis for the displacements ![]() and
and ![]() . They are also covectors (this is easy to verify as they behave like covectors under transformation) so adding them to the normal does not raise said type mismatch. If we divide these terms one more time by
. They are also covectors (this is easy to verify as they behave like covectors under transformation) so adding them to the normal does not raise said type mismatch. If we divide these terms one more time by ![]() and flip their signs, we’ll arrive at the ShaderX5 definition of
and flip their signs, we’ll arrive at the ShaderX5 definition of ![]() and
and ![]() as follows:
as follows:
![]()
![]()
where the hat (as in ![]() ) denotes the normalized normal.
) denotes the normalized normal. ![]() can be interpreted as the normal to the plane of constant
can be interpreted as the normal to the plane of constant ![]() , and likewise
, and likewise ![]() as the normal to the plane of constant
as the normal to the plane of constant ![]() . Therefore we have three normal vectors, or covectors,
. Therefore we have three normal vectors, or covectors, ![]() ,
, ![]() and
and ![]() , and they are the a basis of a cotangent frame. Equivalently,
, and they are the a basis of a cotangent frame. Equivalently, ![]() and
and ![]() are the gradients of
are the gradients of ![]() and
and ![]() , which is the definition I had used in the book. The magnitude of the gradient therefore determines the bump strength, a fact that I will discuss later when it comes to scale invariance.
, which is the definition I had used in the book. The magnitude of the gradient therefore determines the bump strength, a fact that I will discuss later when it comes to scale invariance.
A Little Unlearning
The mistake of many authors is to unwittingly take ![]() and
and ![]() for
for ![]() and
and ![]() , which only works as long as the vectors are orthogonal. Let’s unlearn ‘tangent’, relearn ‘cotangent’, and repeat the historical development from this perspective: Peercy et al. [2] precomputes the values
, which only works as long as the vectors are orthogonal. Let’s unlearn ‘tangent’, relearn ‘cotangent’, and repeat the historical development from this perspective: Peercy et al. [2] precomputes the values ![]() and
and ![]() (the change of bump height per change of texture coordinate) and stores them in a texture. They call it ’normal map’, but is a really something like a ’slope map’, and they have been reinvented recently under the name of derivative maps. Such a slope map cannot represent horizontal normals, as this would need an infinite slope to do so. It also needs some ‘bump scale factor’ stored somewhere as meta data. Kilgard [3] introduces the modern concept of a normal map as an encoded rotation operator, which does away with the approximation altogether, and instead goes to define the perturbed normal directly as
(the change of bump height per change of texture coordinate) and stores them in a texture. They call it ’normal map’, but is a really something like a ’slope map’, and they have been reinvented recently under the name of derivative maps. Such a slope map cannot represent horizontal normals, as this would need an infinite slope to do so. It also needs some ‘bump scale factor’ stored somewhere as meta data. Kilgard [3] introduces the modern concept of a normal map as an encoded rotation operator, which does away with the approximation altogether, and instead goes to define the perturbed normal directly as
![]()
where the coefficients ![]() ,
, ![]() and
and ![]() are read from a texture. Most people would think that a normal map stores normals, but this is only superficially true. The idea of Kilgard was, since the unperturbed normal has coordinates
are read from a texture. Most people would think that a normal map stores normals, but this is only superficially true. The idea of Kilgard was, since the unperturbed normal has coordinates ![]() , it is sufficient to store the last column of the rotation matrix that would rotate the unperturbed normal to its perturbed position. So yes, a normal map stores basis vectors that correspond to perturbed normals, but it really is an encoded rotation operator. The difficulty starts to show up when normal maps are blended, since this is then an interpolation of rotation operators, with all the complexity that goes with it (for an excellent review, see the article about Reoriented Normal Mapping [5] here).
, it is sufficient to store the last column of the rotation matrix that would rotate the unperturbed normal to its perturbed position. So yes, a normal map stores basis vectors that correspond to perturbed normals, but it really is an encoded rotation operator. The difficulty starts to show up when normal maps are blended, since this is then an interpolation of rotation operators, with all the complexity that goes with it (for an excellent review, see the article about Reoriented Normal Mapping [5] here).
Solution of the Cotangent Frame
The problem to be solved for our purpose is the opposite as that of Blinn, the perturbed normal is known (from the normal map), but the cotangent frame is unknown. I’ll give a short revision of how I originally solved it. Define the unknown cotangents ![]() and
and ![]() as the gradients of the texture coordinates
as the gradients of the texture coordinates ![]() and
and ![]() as functions of position
as functions of position ![]() , such that
, such that
![]()
where ![]() is the dot product. The gradients are constant over the surface of an interpolated triangle, so introduce the edge differences
is the dot product. The gradients are constant over the surface of an interpolated triangle, so introduce the edge differences ![]() ,
, ![]() and
and ![]() . The unknown cotangents have to satisfy the constraints
. The unknown cotangents have to satisfy the constraints

where ![]() is the cross product. The first two rows follow from the definition, and the last row ensures that
is the cross product. The first two rows follow from the definition, and the last row ensures that ![]() and
and ![]() have no component in the direction of the normal. The last row is needed otherwise the problem is underdetermined. It is straightforward then to express the solution in matrix form. For
have no component in the direction of the normal. The last row is needed otherwise the problem is underdetermined. It is straightforward then to express the solution in matrix form. For ![]() ,
,
![Rendered by QuickLaTeX.com \[\vec{T} = \begin{pmatrix} \Delta \vec{p_1} \\ \Delta \vec{p_2} \\ \Delta \vec{p_1} \times \Delta \vec{p_2} \end{pmatrix}^{-1} \begin{pmatrix} \Delta u_1 \\ \Delta u_2 \\ 0 \end{pmatrix} ,\]](http://www.thetenthplanet.de/wordpress/wp-content/ql-cache/quicklatex.com-cb56923291b0d70fec82d997de045aa6_l3.png)
and analogously for ![]() with
with ![]() .
.
Into the Shader Code
The above result looks daunting, as it calls for a matrix inverse in every pixel in order to compute the cotangent frame! However, many symmetries can be exploited to make that almost disappear. Below is an example of a function written in GLSL to calculate the inverse of a 3×3 matrix. A similar function written in HLSL appeared in the book, and then I tried to optimize the hell out of it. Forget this approach as we are not going to need it at all. Just observe how the adjugate and the determinant can be made from cross products:
mat3 inverse3x3( mat3 M ) { // The original was written in HLSL, but this is GLSL, // therefore // - the array index selects columns, so M_t[0] is the // first column of M_t, etc. // - the mat3 constructor assembles columns, so // cross( M_t[1], M_t[2] ) becomes the first column // of the adjugate, etc. // - for the determinant, it does not matter whether it is // computed with M or with M_t; but using M_t makes it // easier to follow the derivation in the text mat3 M_t = transpose( M ); float det = dot( cross( M_t[0], M_t[1] ), M_t[2] ); mat3 adjugate = mat3( cross( M_t[1], M_t[2] ), cross( M_t[2], M_t[0] ), cross( M_t[0], M_t[1] ) ); return adjugate / det; } |
We can substitute the rows of the matrix from above into the code, then expand and simplify. This procedure results in a new expression for ![]() . The determinant becomes
. The determinant becomes ![]() , and the adjugate can be written in terms of two new expressions, let’s call them
, and the adjugate can be written in terms of two new expressions, let’s call them ![]() and
and ![]() (with
(with ![]() read as ‘perp’), which becomes
read as ‘perp’), which becomes
![Rendered by QuickLaTeX.com \[\vec{T} = \frac{1}{\left| \Delta \vec{p_1} \times \Delta \vec{p_2} \right|^2} \begin{pmatrix} \Delta \vec{p_2}_\perp \\ \Delta \vec{p_1}_\perp \\ \Delta \vec{p_1} \times \Delta \vec{p_2} \end{pmatrix}^\mathrm{T} \begin{pmatrix} \Delta u_1 \\ \Delta u_2 \\ 0 \end{pmatrix} ,\]](http://www.thetenthplanet.de/wordpress/wp-content/ql-cache/quicklatex.com-14ea900ab796207726424b91a6262eeb_l3.png)
![]()
As you might guessed it, ![]() and
and ![]() are the perpendiculars to the triangle edges in the triangle plane. Say Hello! They are, again, covectors and form a proper basis for cotangent space. To simplify things further, observe:
are the perpendiculars to the triangle edges in the triangle plane. Say Hello! They are, again, covectors and form a proper basis for cotangent space. To simplify things further, observe:
- The last row of the matrix is irrelevant since it is multiplied with zero.
- The other matrix rows contain the perpendiculars (
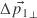 and
and 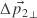 ), which after transposition just multiply with the texture edge differences.
), which after transposition just multiply with the texture edge differences. - The perpendiculars can use the interpolated vertex normal
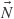 instead of the face normal
instead of the face normal  , which is simpler and looks even nicer.
, which is simpler and looks even nicer. - The determinant (the expression
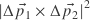 ) can be handled in a special way, which is explained below in the section about scale invariance.
) can be handled in a special way, which is explained below in the section about scale invariance.
Taken together, the optimized code is shown below, which is even simpler than the one I had originally published, and yet higher quality:
mat3 cotangent_frame( vec3 N, vec3 p, vec2 uv ) { // get edge vectors of the pixel triangle vec3 dp1 = dFdx( p ); vec3 dp2 = dFdy( p ); vec2 duv1 = dFdx( uv ); vec2 duv2 = dFdy( uv ); // solve the linear system vec3 dp2perp = cross( dp2, N ); vec3 dp1perp = cross( N, dp1 ); vec3 T = dp2perp * duv1.x + dp1perp * duv2.x; vec3 B = dp2perp * duv1.y + dp1perp * duv2.y; // construct a scale-invariant frame float invmax = inversesqrt( max( dot(T,T), dot(B,B) ) ); return mat3( T * invmax, B * invmax, N ); } |
Scale invariance
The determinant ![]() was left over as a scale factor in the above expression. This has the consequence that the resulting cotangents
was left over as a scale factor in the above expression. This has the consequence that the resulting cotangents ![]() and
and ![]() are not scale invariant, but will vary inversely with the scale of the geometry. It is the natural consequence of them being gradients. If the scale of the geomtery increases, and everything else is left unchanged, then the change of texture coordinate per unit change of position gets smaller, which reduces
are not scale invariant, but will vary inversely with the scale of the geometry. It is the natural consequence of them being gradients. If the scale of the geomtery increases, and everything else is left unchanged, then the change of texture coordinate per unit change of position gets smaller, which reduces ![]() and similarly
and similarly ![]() in relation to
in relation to ![]() . The effect of all this is a diminished pertubation of the normal when the scale of the geometry is increased, as if a heightfield was stretched.
. The effect of all this is a diminished pertubation of the normal when the scale of the geometry is increased, as if a heightfield was stretched.
Obviously this behavior, while totally logical and correct, would limit the usefulness of normal maps to be applied on different scale geometry. My solution was and still is to ignore the determinant and just normalize ![]() and
and ![]() to whichever of them is largest, as seen in the code. This solution preserves the relative lengths of
to whichever of them is largest, as seen in the code. This solution preserves the relative lengths of ![]() and
and ![]() , so that a skewed or stretched cotangent space is sill handled correctly, while having an overall scale invariance.
, so that a skewed or stretched cotangent space is sill handled correctly, while having an overall scale invariance.
Non-perspective optimization
As the ultimate optimization, I also considered what happens when we can assume ![]() and
and ![]() . This means we have a right triangle and the perpendiculars fall on the triangle edges. In the pixel shader, this condition is true whenever the screen-projection of the surface is without perspective distortion. There is a nice figure demonstrating this fact in [4]. This optimization saves another two cross products, but in my opinion, the quality suffers heavily should there actually be a perspective distortion.
. This means we have a right triangle and the perpendiculars fall on the triangle edges. In the pixel shader, this condition is true whenever the screen-projection of the surface is without perspective distortion. There is a nice figure demonstrating this fact in [4]. This optimization saves another two cross products, but in my opinion, the quality suffers heavily should there actually be a perspective distortion.
Putting it together
To make the post complete, I’ll show how the cotangent frame is actually used to perturb the interpolated vertex normal. The function perturb_normal does just that, using the backwards view vector for the vertex position (this is ok because only differences matter, and the eye position goes away in the difference as it is constant).
vec3 perturb_normal( vec3 N, vec3 V, vec2 texcoord ) { // assume N, the interpolated vertex normal and // V, the view vector (vertex to eye) vec3 map = texture2D( mapBump, texcoord ).xyz; #ifdef WITH_NORMALMAP_UNSIGNED map = map * 255./127. - 128./127.; #endif #ifdef WITH_NORMALMAP_2CHANNEL map.z = sqrt( 1. - dot( map.xy, map.xy ) ); #endif #ifdef WITH_NORMALMAP_GREEN_UP map.y = -map.y; #endif mat3 TBN = cotangent_frame( N, -V, texcoord ); return normalize( TBN * map ); } |
varying vec3 g_vertexnormal; varying vec3 g_viewvector; // camera pos - vertex pos varying vec2 g_texcoord; void main() { vec3 N = normalize( g_vertexnormal ); #ifdef WITH_NORMALMAP N = perturb_normal( N, g_viewvector, g_texcoord ); #endif // ... } |
The green axis
Both OpenGL and DirectX place the texture coordinate origin at the start of the image pixel data. The texture coordinate (0,0) is in the corner of the pixel where the image data pointer points to. Contrast this to most 3‑D modeling packages that place the texture coordinate origin at the lower left corner in the uv-unwrap view. Unless the image format is bottom-up, this means the texture coordinate origin is in the corner of the first pixel of the last image row. Quite a difference!
An image search on Google reveals that there is no dominant convention for the green channel in normal maps. Some have green pointing up and some have green pointing down. My artists prefer green pointing up for two reasons: It’s the format that 3ds Max expects for rendering, and it supposedly looks more natural with the ‘green illumination from above’, so this helps with eyeballing normal maps.
Sign Expansion
The sign expansion deserves a little elaboration because I try to use signed texture formats whenever possible. With the unsigned format, the value ½ cannot be represented exactly (it’s between 127 and 128). The signed format does not have this problem, but in exchange, has an ambiguous encoding for −1 (can be either −127 or −128). If the hardware is incapable of signed texture formats, I want to be able to pass it as an unsigned format and emulate the exact sign expansion in the shader. This is the origin of the seemingly odd values in the sign expansion.
In Hindsight
The original article in ShaderX5 was written as a proof-of-concept. Although the algorithm was tested and worked, it was a little expensive for that time. Fast forward to today and the picture has changed. I am now employing this algorithm in real-life projects for great benefit. I no longer bother with tangents as vertex attributes and all the associated complexity. For example, I don’t care whether the COLLADA exporter of Max or Maya (yes I’m relying on COLLADA these days) output usable tangents for skinned meshes, nor do I bother to import them, because I don’t need them! For the artists, it doesn’t occur to them that an aspect of the asset pipeline is missing, because It’s all natural: There is a geometry, there are texture coordinates and there is a normal map, and just works.
Take Away
There are no ‘tangent frames’ when it comes to normal mapping. A tangent frame which includes the normal is logically ill-formed. All there is are cotangent frames in disguise when the frame is orthogonal. When the frame is not orthogonal, then tangent frames will stop working. Use cotangent frames instead.
References
[1] James Blinn, “Simulation of wrinkled surfaces”, SIGGRAPH 1978
http://research.microsoft.com/pubs/73939/p286-blinn.pdf
[2] Mark Peercy, John Airey, Brian Cabral, “Efficient Bump Mapping Hardware”, SIGGRAPH 1997
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.42.4736
[3] Mark J Kilgard, “A Practical and Robust Bump-mapping Technique for Today’s GPUs”, GDC 2000
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.18.537
[4] Christian Schüler, “Normal Mapping without Precomputed Tangents”, ShaderX 5, Chapter 2.6, pp. 131 – 140
[5] Colin Barré-Brisebois and Stephen Hill, “Blending in Detail”,
http://blog.selfshadow.com/publications/blending-in-detail/
Out of interest, what implications does this have for tangent-space calculations when you *bake* normal-maps (for example, inside 3dsmax).
Wouldn’t you have to also use this method when creating the original normal-map?
Hi MoP, absolutely, you’re correct in your assumption.
If your normal map is the result of sampling high poly geometry, then the normal map sampler should use the same assumptions about tangent space than the in the engine, if you want highest fidelity. This is generally true, whether you use precomputed tangents or not.
If on the other hand you have a painted normal map, let’s say, a generic ripple texture, this just follows whatever texture mapping is applied to the mesh. If this mapping is sheared or stretched, and so violates the square patch assumption, the algorithm from above is still able to light it correctly.
Thanks for the fast reply, Christian!
Absolutely, that makes sense… so I’m wondering if, for “perfect” results, if people are baking their normal maps in 3dsmax or Maya or XNormal or whatever, those programs will need to have their tangent space calculations updated/reworked to match the in-game calculation?
I’m guessing that currently the 3dsmax calculation is not exactly synced with the method you describe here… or am I wrong?
You would be surprised to know that the method in 3dsMax or anywhere else is most likely not synced with any engine, even when using the classic method. There is an entire thesis devoted to this topic (look for Mikkelsen here). If you want such perfection, then the engine should have its own tools for baking normal maps because only then it is going to know what their shaders do. 3dsMax can never know this!
Yep, that makes sense — in fact that’s what the Doom 3 engine (id Tech 4) did to ensure the normal maps were perfect … they imported LWOs into the engine and baked the normal-maps using the game engine so that the calculations would match up perfectly.
I haven’t seen any other engine (released publically) do that yet, but I work in game development and I know that we have been trying to solve this problem for years with no satisfactory results. Currently the best method seems to be to modify a third-party program (eg. XNormal) to calculate tangent space in exactly the same way as the target engine calculates it, as this is the only way to ensure the normal-maps will be absolutely correct.
Pingback: Normal Mapping Without Precomputed Tangents « Interplay of Light
I am confused to what space your TBN matrix the normal from the normal map texture converts! You need this in order to do lighting calculations. Should I transform the light vector and view vector with the TBN matrix, or leave them in camera space?
Do you assume in the fragment shader that g_vertexnormal, g_viewvector are in the vertex shader multiplied with the gl_NormalMatrix and gl_ModelViewMatrix respectively? Otherwise how do you account for the transformations on the object.
Thanks
Sorry I meant in the previous post “light vector” and “eye vector” instead of view vector for the fist paragraph.
Hi cinepivates,
the TBN matrix that I build in the pixel shader is the transform from cotangent space to world space. After the vector from the normal map is multiplied with the TBN matrix, it is a world space normal vector. This is due to the fact that both the interpolated vertex normal and the view vector are supplied in world space by the vertex shader (not shown). Alternatively, if the vertex shader supplies these vectors in eye space, the pixel shader should construct the TBN matrix to convert into eye space instead. So you can choose your way.
Hi
thanks for the reply.
Since you are multiplying per pixel with a mat3 (TBNxNormal) on the pixel shader have you measured any performance decrease compared to the more traditional method of precomputed Tangents where you usually only transform in the vertex shader the light,eye vectors into tangent space using the TBN matrix.
I don’t use the TBN in the vertex shader. That is a thing of the past when there was pixel shader model 1.x. It prevents you to use world space constants in the pixel shader. For example, a reflection vector to look up a world space environment map. So the matrix multiply by TBN in the pixel shader has always been there for me.
Hi,I just wondering if lighting calculations can be done in tangent space.My textures could not match the Square Patch Assumption,but I don’t want to lose tangent space lighting,since some techniques are particular designed for that.
Hi April, and
and  ) will change under a non-orthogonal transformation. So
) will change under a non-orthogonal transformation. So  ,
,  ,
,  and any other vector you need into tangent space, and do the lighting computations there.
and any other vector you need into tangent space, and do the lighting computations there.
this is tricky, as lighting in tangent space does only work if it is orthogonal. Think about it: the angle between any vectors (say, the angle between
dot(N,L)is going to result in a different value, depending on which space it is in. If you can live with that, then take the inverse-transpose of the TBN matrix (this is in essence what you get when you do the non-perspective optimization mentioned in the post), and use that to transformThanks for reply :)
I managed to orthogonalize the matrix and then used the inverse-transpose one to do lighting in world space, the result became a mess.I checked the orgin matrix, and found out the matrix can not be inversed where UV mirrors. The determinant() function returns 0.
Still looking for reason.
I’m not sure I can follow your argument. If you want to do lighting in world space, then you don’t need to change anything. If you want to do lighting in tangent space instead (which only yields similar results if the tangent space is roughly orthogonal), you’d need a matrix to convert your light, view, etc vectors into tangent space. Edit: For this you need the inverse of the TBN. You can get the inverse-tranpose already very simply by ignoring the two cross products and using
dp2perp = dp1anddp1perp = dp2. Then the transpose of this would be the inverse of the TBN (ignoring scale). In the shader you don’t need to explicitly transpose, you can just multiply with the vectors from the left (egvector * matrixinstead oftranspose(matrix) * vector). Then you can orthogonalize this matrix if you want, but this won’t help much if the tangent space is not orthogonal to begin with. I don’t understand why you are willing to go though such hoops instead of simply doing the lighting in world space.Fantastic article! I switched my engine from using precalculated tangents to the method your describe — very easy to implement. I’m using WebGL, but I’m presuming my findings will correspond to what OpenGL + GLES programmers see. On desktop, I don’t really notice much of a performance difference (if anything, the tangent-less approach is slightly slower). But on mobile (tried on both Galaxy Nexus and Nexus 7), this method roughly twice as slow as using precomputed tangents. Seems dFdx and dFdy are particularly slow on mobile GPUs. Just cutting out those calls takes my FPS from ~24FPS to ~30FPS. So although I think this method is elegant to the extreme, I’m not sure it’s fast enough to be the better option (at least, not on mobile). I really hope someone can convince me otherwise though! :)
Hi Will, thanks for sharing. Of course those additional ~14 shader instructions for
cotangent_frame()are not free, especially not on mobile (which is like 2005 desktop, the time when the article was originally written). For me today, this cost is invisible compared to all the other things that are going on, like multiple lights and shadows and so forth. On the newest architectures like the NVidia Fermi, it could already be a performance win to go without precomputed tangents, due to the reasons mentioned in the introduction. But while that is nice, the main reason I use the method is the boost in productivity.Pingback: Martin Codes – Cool Link Stash, January 2013
For me the equations in this are screwed up. The are random LaTeX things in the images (Deltamathbf). Same with Safari, Chrome and Firefox.
Would be nice if you could fix that.
Something wrong with formulas. Maybe math plugin is broken?
Hallo there, I have fixed the math formulae in the post. It turned out to be an incompatibility between two plugins, and that got all backslashes eaten. Sorry for that! Should there be a broken formula that I have overlooked, just drop a line.
backslashes eaten. Sorry for that! Should there be a broken formula that I have overlooked, just drop a line.
So glad I found your blog. Though I am an artist these more technical insights really help me in understanding what to communicate to our coders to establish certain looks.
You’re welcome!
Hi, I want to ask you to elaborate on 2 following moments. First of all I would like to know why cross(N,Pv)/length(N)=gradient(u) and cross(Pu, N)/length(N)=gradient(v). I just can not find any mathematical derivation of this fact. Also it is unclear for me why deltaU = dot(T, deltaP), and how this follows from definition of gradient. Otherwise I found this article very exciting and my experiments showed that implementation works very well and is a good drop-in replacement for conventional tangent basis.
Hi Mykhailo,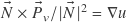 , and that may not be obvious, so here it goes: The gradient vector is always perpendicular to the iso-surface (aka. “level-set”). In a skewed 2‑D coordinate system, the iso-line of one coordinate is simply the other coordinate axis! So the gradient vector for the
, and that may not be obvious, so here it goes: The gradient vector is always perpendicular to the iso-surface (aka. “level-set”). In a skewed 2‑D coordinate system, the iso-line of one coordinate is simply the other coordinate axis! So the gradient vector for the  texture coordinate must be perpendicular to the
texture coordinate must be perpendicular to the  axis, and vice versa. (The scale factor makes it such that the overall length equals the rate of change, which is dependent on the assumption that
axis, and vice versa. (The scale factor makes it such that the overall length equals the rate of change, which is dependent on the assumption that  .) Your second question is also related to the fact that the gradient vector is perpendicular to the iso-surface. If a position delta is made parallel to the iso-surface, then the texture coordinate doesn’t change, because in this case the dot product is zero.
.) Your second question is also related to the fact that the gradient vector is perpendicular to the iso-surface. If a position delta is made parallel to the iso-surface, then the texture coordinate doesn’t change, because in this case the dot product is zero.
thanks for sharing your experience. Indeed, I did not explain why
Thank you for an answer, now everything is a bit clearer. Still was able to fully figure it out only after I understood that parametrisation of u, v is linear in the plane of every triangle. For some reason I just missed that fact. And after you mentioned that gradient is perpendicular to iso-line everything made sense. And now it make sense why change of u is projection of position delta onto gradient vector.
Hi Christian, thanks for sharing!
I am working on an enhanced version of the Crytek-Sponza scene and I had problems with my per-pixel normalmapping shader based on precomputed tangents. I had most surfaces lighted correctly, but in some cases they weren’t. It turned out that — unknown to me — some faces had flipped UVs (which is not that uncommon) and therefore the cotangent frame was messed up, because the inverse of the tangent was used to calculate the binormal as the crossproduct with the vertex normal.
Now, I replaced it with your approach and everything is alright; it works instantly and all errors vanished. Awesome!! :-)
Thanks
Hi,
Does the computation still work if the mesh normal is in view space, and the g_viewvector = vec3(0, 0, ‑1) ?
Cheers :)
Yes, but you must provide the vertex position in view space also. The view vector is used as a proxy to differentiate the vertex position, therefore a constant view vector will not do.
Ah ok, I just normalized the view position and its working perfectly
Thanks!
Hi,
Your idea seem to be very interesting.
But I’ve tried it in real scene, and found a glitch — if uv (texture coordinates) are mirrored, normal is also become mirrored.
Is there any way to fix it?
The normal itself should not be flipped, only the tangents. If the texture coordinate is mirrored, then the
texture coordinate is mirrored, then the  tangent should reverse sign and similar with
tangent should reverse sign and similar with  and the
and the 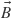 tangent.
tangent.
In the code you show in the article, you’re using ‑V as the position for taking derivatives. But V is normalized per-pixel, so your position derivatives effectively have their radial component (toward/away from the camera) projected out. Doesn’t this create some artifacts when the surface is at a glancing angle to the camera?
(You also lose scale information, but since you’re normalizing to make it scale-invariant anyway, I suppose this does not matter.)
Hi Nathan the article doesn’t mention it explicitly but the view vector is meant to be passed unnormalized from vertex to pixelshader. The normalization should happen after it has been used to compute the cotangent frame.
(EDIT: I corrected the normalization mistake in the example code, now code + text are in agreement)
Hello Christian,
What can be done with the texcoords if we sample from 2 normal maps with different uv’s
We add them? or? i guess the rate of change will be the same
Example code is:
float3 normal1 = tex2d(normalmap1, 3*uv1);
float3 normal2 = tex2d(normalmap2, 5*uv2);
float3 normal = normalize (lerp(normal1, normal2, 0.5f) );
Remarks: This operation is not good blending at all and my question is, if it was, how i will can use the uv’s?
Best Regards
float2 uv_for_perturbation_function = lerp(3*uv1, 5*uv2, 0.5f)
Like this?
Hi Stefan,
I assume that the mapping of uv1 and uv2 is different. Then you are going to need a tangent frame for each, transform both normals into a common space (here: world space) and then mix them.
float3 normalmap1 = tex2d(normalmap1, uv1);
float3 normalmap2 = tex2d(normalmap2, uv2);
float3x3 TBN1 = cotangent_frame( vertex_normal, -viewvector, uv1 );
float3x3 TBN2 = cotangent_frame( vertex_normal, -viewvector, uv2 );
float3 normal = normalize( lerp( mul( TBN1, normalmap1 ), mul( TBN2, normalmap2 ), 0.5f ) );
etc
hope this helps
Hello,
I try to do importance sampling of the Beckmann Distribution of a Cook Torrance BRDF. I use your description to create a TBN-Matrix in order to transform the halfvector from tangent-space to world-space.
The problem is that I can see every fragment (triangle) of my geometry and not a glossy shaded surface. I’m not sure if the problem is really connected with the TBN-Matrix. Does it work for lighting calculations without restrictions? Or do you think I have to search the mistake somewhere else?
Hallo Phil, and
and 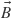 , are going to be faceted (aka ‘flat shaded’). However the normal vector
, are going to be faceted (aka ‘flat shaded’). However the normal vector 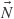 is not. So unless you use are very low specular exponent (high RMS slope in case of Beckmann) it should not visually matter.
is not. So unless you use are very low specular exponent (high RMS slope in case of Beckmann) it should not visually matter.
the partial derivatives of texture coordinates (the dFdx and dFdy instructions) are constant over the surface of a triangle, so both tangent directions,
I tried this, but am having some problems.
I’m using a left-handed coordinate system and I provide the normal and the view vector in view space. It seems from one of the comments, that this should work.
At first I though every is looking good, but than I noticed, that the perturbed normals are not quite right in some cases. Lighting code should be fine, because results with unperturbed normals look as expected.
If I use the cotangent frame to transform the view vector into cotangent space for parallax mapping, the results look correct as well.
I’m also using D3D-style UVs where (0,0) is the top left corner, but that should not matter, right?
Any ideas what could wrong?
Hi Benjamin, and
and  , that’s all.
, that’s all.
as I said in the article, the texture coordinate origin is at the start of the image array in both OpenGL and D3D so the UV mirroring must be done in both APIs. If your coordinate system is left handed, you’ll need to negate both
I’ve tried implementing this, but found that you get a faceted appearance on the world space normal, presumably due to the derivatives being per-triangle. Am I doing something wrong, or is this a limitation of this technique?
Hi James,
as some other people have commented, the tangential directions are faceted, due to fact tha partial derivatives (dFdx) of texture coordinates are constant per triangle. However for the normal direction the interpolated normal is used so the faceting can only appears if there is a difference in the UV gradients from one triangle to the next.
Could you please post your vertex shader code? I’m doing something dumb wrong and I’ve been trying to get this to work all day.
Hi Rob,
there is really nothing to the vertex shader, just transforms. Below is an example (transforms[0] is the model-to-world transform and transforms[1] is world-to-clip).
uniform mat4 transforms[2];
uniform vec4 camerapos;
varying vec2 texcoord;
varying vec3 vertexnormal;
varying vec4 viewvector;
void main()
{
vec4 P = transforms[0] * gl_Vertex;
gl_Position = transforms[1] * P;
texcoord = gl_MultiTexCoord0.xy;
vertexnormal =
( transforms[0] * vec4( gl_Normal, 0. ) ).xyz;
viewvector = camerapos — P;
}
Ohhh, I was hoping my problem might be in the vertex shader code but that’s what I have.
The problem I have is that if I use the normal from perturb_normal, the lighting rotates with the model so it is always the same side of the model that is lit (beautifully) no matter how the model is oriented relative to the light source. If I light the model with just the interpolated vertex normal I get lighting which works as expected.
I wrote out the details of what I’m doing at http://onemanmmo.com/index.php?cmd=newsitem&comment=news.1.158.0 I’m going to have to look at this again tomorrow to see if I can figure out what it is I’m doing wrong. Thank you for your help.
(This is a follow-up to my previous post, but I can’t find out how to reply to your reply.)
I noticed you saying
“Hi Nathan the article doesn’t mention it explicitly but the view vector is meant to be passed unnormalized from vertex to pixelshader. The normalization should happen after it has been used to compute the cotangent frame.” In one of the replies.
In the code however the view vector is normalized before it is passed to perturbNormal(). Isn’t this contradictory?
The reason I’m asking is that I’m still struggling to get this working for view space normals. If the normalmap only contains (0, 0, 1), the final perturbed normal is unchanged and everything works as expected, as the normal effectively is not perturbed at all.
Perturbing by (0, 1, 0) however gives me strange results for instance. It is especially noticeable at grazing angles. Looking at a plane there is a vertical line where the normal suddenly flips drastically although the surface normal did not change at all.
I tried flipping B and T etc., but the “flipping” effect is not immediately related to this.
Hi Benjamin,
thanks for the suggestion, that’s a serious gotcha, and I corrected it.
The code that I posted should pass
g_viewvectorinto the functionperturb_normal.If you follow the argument in the article it should be obvious:
perturb_normalofficially wants the vertex position, but any constant offset to that is going to cancel when taking the derivative. Therefore, the view vector can be passed in as a surrogate of the vertex position, but this is only true of the unnormalized view vector.Have you tried that?
(BTW, while you cannot reply to my reply, you can reply to your original comment. The maximum nesting level here is 2)
That solved it. Thanks for your helpful answers!
Hi,
I’m new to shaders, but I have to implement some features in a webGL project (based on this template: http://learningwebgl.com/lessons/lesson14/index.html)
I have already implemented a specular map, but here are some new things and another shader language.
What I actually want to ask:
— where comes the ‘mapBump’ from? Is it already implemented in GLSL (and webGL)?
— How does ‘map = map * 255./127. — 128./127.;’ work? What means the ‘.’ after each number?
Nevermind!
In the end, everything was self-explaning.
Also I just got it working.
The webGL shader language seems to be a bit immature which caused many issues, but finally, I got it working.
Thanks for the great tutorial!
Hallo Basti,
WebGL is modeled after OpenGL ES (and not Desktop OpenGL), so there may be some incompatibilities. But the shading language as such should be the same GLSL. Of course, the name ‘mapBump’ is only an example and you can use any old name. You should be able to leave out a leading or trailing zero in floating point numbers, so you can write 2. instead of 2.0 etc.
Hi Christian,
Thank you for writing this article to explain the concept of the cotangent frame, and also for your attention to implementation efficiency details.
I’m still hazy on a number of things though, especially these two:
1.) In the Intermission 2 section, you write:
T = cross(N, Pv)/length(N)^2 = gradient(u)
B = cross(Pu, N)/length(N)^2 = gradient(v)
You seem to imply that if the tangent frame is orthogonal, T = Pu and B = Pv, and the differences only occur when the frame has skew. However, I’m confused about the conventions you’re using: If we assume cross products follow the right-hand rule, and if we assume Pu points right and Pv points up, then T = ‑Pu and B = ‑Pv for an orthogonal tangent frame. In other words, T = Pu and B = Pv only holds for orthogonal tangent frames if either:
a.) We’re using the left-hand rule (thank you Direct3D for ruining consistent linear algebra conventions forever)
b.) Pv points down (i.e. the texture origin is in the top-left corner, rather than the bottom right corner)
…but not both.
What convention/assumption are you using for the above relationships? Are you using the same conventions/assumptions throughout the rest of the mathematical derivation? Would it be more appropriate in a pedagogical sense to swap the order of the cross products, or am I missing something important?
2.) I don’t have the background to deeply understand the precise difference between a tangent frame and a cotangent frame. Here is the extent of my background knowledge on the subject:
a.) Surface normals are covectors/pseudovectors, whatever the heck that means.
b.) Covectors/pseudovectors like normals transform differently from ordinary vectors. Consider matrix M, column vector v, and normal [column] vector n in the same coordinate frame as v. If you use mul(M, v) to transform v into another coordinate frame, you need to use mul(transpose(inverse(M)), n) to transform the normal vector. This reduces to mul(M, n) if M is orthogonal, but otherwise the inverse-transpose operation is necessary to maintain the normal vector’s properties in the destination frame (specifically, to keep the normal vector perpendicular to the surface). I’ve taken this for granted for some time, but I don’t have a deep understanding of why the inverse-transpose is the magic solution for transforming normal vectors, and I believe this might be why I’m having trouble understanding the nature of the cotangent frame.
Now, if I were to create a “traditional” TBN matrix from derivatives, I’d do it roughly like this (no optimization, for clarity…and forgive me if some Cg-like conventions slip through):
vec3 dp1 = dFdx( p );
vec3 dp2 = dFdy( p );
vec2 duv1 = dFdx( uv );
vec2 duv2 = dFdy( uv );
// set up a linear system to solve for the TBN matrix:
vec3 p_mat = mat3(dp1, dp2, N);
vec3 uv_mat = mat3(duv1, duv2, vec3(0.0, 0.0, 1.0));
// TBN transforms [regular, non-normal] vectors from
// tangent space to worldspace, so:
// p_mat = mul(TBN, uv_mat)
// therefore, solve as:
mat3 TBN = mul(p_mat, inverse(uv_mat));
// example transforms:
vec3 arbitrary_worldspace_vector = mul(TBN, arbitrary_tangent_space_vector);
vec3 worldspace_normal = mul(transpose(inverse(TBN)), normal_map_val);
First, a quick question: Due to the inverse-transpose operation, this blatantly inefficient “traditional TBN” solution should work correctly even for non-orthogonal TBN matrices, correct?
Anyway, it follows from the nature of the tangent-to-worldspace transformation that p_mat = mul(TBN, uv_mat) above. After all, the whole point of the worldspace edges is that they’re the uv-space edges transformed from tangent-space to worldspace.
For this reason, I still share some of the confusion of the poster at http://www.gamedev.net/topic/608004-computing-tangent-frame-in-pixel-shader/. You mentioned the discrepancy has to do with your TBN matrix being a cotangent frame composed of covectors, but I’m not yet clear on the implications of that.
However, I noticed something interesting that I’m hoping will make everything fall into place: You transform your normal vector *directly* from tangent-space to worldspace using your cotangent frame. That is, you just do something like:
vec3 worldspace_normal = mul(cotangent_TBN, normal_map_val);
Is the your cotangent frame TBN matrix simply the inverse-transpose of the traditional tangent frame TBN matrix? If so, and correct me if I’m wrong here…if you wanted to transform ordinary vectors like L and V from worldspace to tangent-space (for e.g. parallax occlusion mapping), you would simply do:
tangent_space_V = mul(transpose(cotangent_TBN), worldspace_V);
If I’m understanding all this correctly, constructing your cotangent frame is inherently more efficient than the traditional TBN formulation for non-orthogonal matrices: It lets us transform [co]tangent-space normals to worldspace normals with a simple TBN multiplication (instead of an inverse-transpose TBN multiplication), and it lets us transform ordinary vectors from worldspace t [co]tangent-space with a transpose-TBN multiplication instead of an inverse-TBN multiplication.
Do I have this correct, or is the cotangent frame matrix something entirely different from what I am now thinking?
Hi Michael,
that’s a hand full of a comment so i’m trying my best to answer.
(1)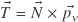 has the cross product backwards, and I should correct it in the article. Note that the code in the shader does the right thing, e.g. it says
has the cross product backwards, and I should correct it in the article. Note that the code in the shader does the right thing, e.g. it says  behaves the way I describe it.
behaves the way I describe it.
Good observation! The formula which says
dp2perp = cross( dp2, N ), since my derivation is based on the assumption thatSo since I took the formula out of Blinns Paper, I checked it to see what he has to says about his cross product business — and in one of his drawings, the vector is indeed in the opposite direction as
is indeed in the opposite direction as  :
:
(2) ). The
). The 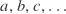 behave like any old vector space and so they’re called the coordinates of a co-vector, while the
behave like any old vector space and so they’re called the coordinates of a co-vector, while the 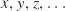 are the coordinates of an ordinary vector.
are the coordinates of an ordinary vector.
Co-vectors are a fancy name for “coordinate functions”, i.e. plane equations (as in
The ordinary vector tells you “the x axis is in this direction”. The co-vector tells you the function for the x‑coordinate.
If you have a matrix of column basis vectors, then the rows of the inverse matrix are the co-vectors, the plane equations that give the coordinate functions.
If you stick with the distinction to treat co-vectors as rows, you don’t need any of this “inverse transpose” business — just the ordinary inverse will do, and you multiply normal vectors as rows from the left.
(2b)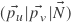 , then yes, you would need to take the inverse (transpose) of that to correctly transform a normal vector in the general case. But the whole point of the article is to construct the TBN matrix as
, then yes, you would need to take the inverse (transpose) of that to correctly transform a normal vector in the general case. But the whole point of the article is to construct the TBN matrix as  instead, which you can use directly, since it is a co-tangent frame!
instead, which you can use directly, since it is a co-tangent frame!
If your TBN matrix was constructed as
The author of the post at http://www.gamedev.net/topic/608004-computing-tangent-frame-in-pixel-shader/ uses the asterisk symbol “*” to describe a matrix product in the first case, and a dot product in the second case. He wonders why, seemingly, the formula to compute the same thing has the “product” on different sides by different authors. That’s his “discrepancy”. The truth is: The formulae do not compute the same thing!
Yes, you can say that and
and 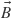 are the “inverse-transpose” of
are the “inverse-transpose” of  and
and  . The third one,
. The third one, 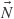 , does not change direction under the inverse-transpose operation, since it is orthogonal to the other two. And if it is unit length, it will stay unit length.
, does not change direction under the inverse-transpose operation, since it is orthogonal to the other two. And if it is unit length, it will stay unit length.